参考:Kruger Timm等编著的 The lattice boltzmann method, principles and practice, 2017.
在流体力学中,最常见的固液边界是无滑移速度边界。最早的固体边界处理方式是反弹,由于它简单易实现,目前仍然是最广泛应用的边界处理方式。
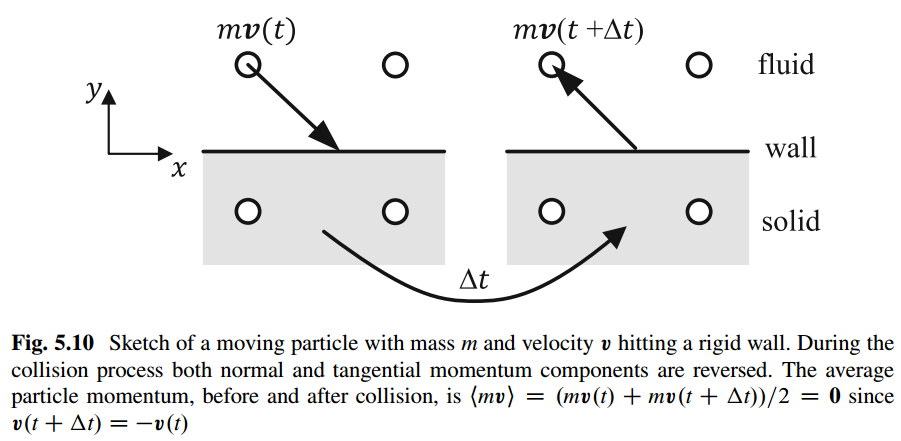
反弹边界(Bounce-Back)原理
简单地解释反弹边界,即粒子在传播过程中撞击固体壁面后,会回到它们来的方向。如果我们把粒子想象成体现流体物质的部分,我们就可以理解这一点。由此可见,粒子撞击墙壁的反弹意味着没有穿过边界的流量,即墙壁对流体是不可渗透的。同样,粒子被反弹而不是被向前反弹(即镜面反射)的事实意味着流体和边界之间没有相对的横向运动,即流体不会在墙上滑动。这两点说明了粒子水平上的反弹方法是如何反映墙面上宏观速度的Dirichlet边界条件的。严格解释反弹规则的宏观行为需要使用多尺度扩展技术,如Chapman-Enskog分析。
全步长反弹(fullway bounce-back)和半步长反弹(halfway bounce-back)
反弹方法分为两种,全步长反弹中粒子会经过边界到固体节点的整个路径,粒子速度在下一个碰撞步翻转。半步长反弹中,粒子只经过边界点到固体点一半的距离,因此速度翻转与streaming是同一个时间步。
这两种方法都引入了对LB算法的具体修改。全步长反弹法需要在固体节点上存储流动步的结果,然后在接下来的碰撞步骤中反弹回来。而在半步长反弹中,由于反转发生在流动步骤中,所以固体节点是不必要的。在算法上,我们可以说,全步长反弹法改变了固体节点的碰撞,但却没有改变通常的流动,而半步长反弹法则改变了流动,没有修改碰撞。
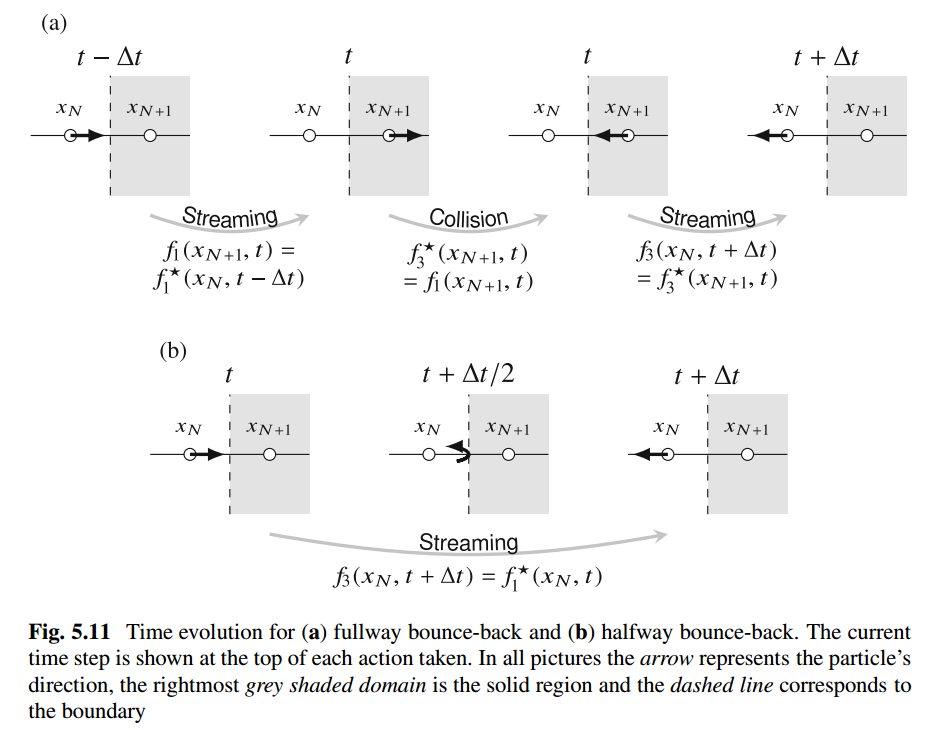
尽管它们的名字是fullway和halfway,两种方法都假定边界位于固体和边界节点之间的大约中间位置,而不是在固体节点本身。
全步长反弹具有一阶精度,半步长反弹有二阶精度。
注:对于全步长反弹,只需要检查目前是否在固体节点上。在算法实现上,对于每一个节点是一个if语句。对于半步长反弹,需要检查每个迁移方向,例如,判断该迁移方向上是固体节点(这意味着需要进行反弹),还是液体或边界点(意味着需要进行正常的流动)。例如,对于D3Q19的模型,半步长反弹会产生18个if语句。