S.J.P. Callens, R.J.C. Uyttendaele, L.E. Fratila-Apachitei, A.A. Zadpoor, Substrate curvature as a cue to guide spatiotemporal cell and tissue organization, Biomaterials. 232 (2020) 119739.
Recent evidence clearly shows that cells respond to various physical cues in their environments, guiding many cellular processes and tissue morphogenesis, pa- thology, and repair. One aspect that is gaining significant traction is the role of local geometry as an extracellular cue. Elucidating how geometry affects cell and tissue behavior is, indeed, crucial to design artificial scaffolds and understand tissue growth and remodeling. Perhaps the most fundamental descriptor of local geometry is surface curvature, and a growing body of evidence confirms that surface curvature affects the spatiotemporal organization of cells and tissues. While well-defined in differential geometry, curvature remains somewhat ambiguously treated in biological studies. Here, we provide a more formal curvature framework, based on the notions of mean and Gaussian curvature, and summarize the available evidence on curvature guidance at the cell and tissue levels. We discuss the involved mechanisms, highlighting the interplay between tensile forces and substrate curvature that forms the foundation of curvature guidance. Moreover, we show that relatively simple computational models, based on some application of curvature flow, are able to capture experimental tissue growth remarkably well. Since curvature guidance principles could be leveraged for tissue regeneration, the implications for geometrical scaffold design are also discussed. Finally, perspectives on future research opportunities are provided.
最近的研究发现,细胞相应于环境中的多种物理因素。其中一个重要的因素是局部几何形态。阐明几何学如何影响细胞和组织的行为,是设计支架和理解组织生长和重塑的关键。或许局部几何形态的最基本描述是曲率。在生物学研究中,曲率的处理仍然有些模糊不清。
本文提出一种更正式的曲率框架,基于平均曲率和高斯曲率,并总结了现有的关于曲率引导细胞和组织的证据。
理解曲率
曲率是一种基本的几何属性,可以提供关于形状的局部信息。在组织生长的研究中,通常采用“concavity”和“convexity”这样模糊的词来处理曲率的问题。二维平面上的曲线,每一点都可以计算曲率,也就是该点相切圆的半径的倒数。三维下类似,单个点上的曲率描述了表面在该点如何偏离切平面。这意味着曲率是表面的局部属性。
两个重要的概念:平均曲率和高斯曲率
To quantitatively describe surface curvature, two important measures have been established, namely the mean curvature, H, and the Gaussian curvature, K, both of which are useful and provide complementary perspectives on curvature.
在曲面上取一点E,曲面在E点的法线为z轴,过z轴可以有无限多个剖切平面,每个剖切平面与曲面相交,其交线为一条平面曲线,每条平面曲线在E点有一个曲率半径。不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。这些曲率半径中,有一个最大和最小的曲率半径,称之为主曲率半径,记作 k1 与 k2,相应地有两个主曲率 κ1和κ2。
然后可以使用主曲率定义平均曲率和高斯曲率:
这两个曲率量纲都是一维的,平均曲率为1/l,高斯曲率为1/l^2。显然,一个平面的平均曲率和高斯曲率都是0,一个圆柱的平均曲率是非零的,而高斯曲率为0。为了获得非零的高斯曲率,两个主曲率必须都非零。
重要的一点是,高斯曲率的符号是表示一个表面类型的重要指标,因为无论考虑哪一侧,高斯曲率的符号都保持不变。例如无论从球面的外部还是内部,球上点的高斯曲率始终为正。而平均曲率的符号取决于表面法线的方向。平均曲率和高斯曲率的更深层差异是,平均曲率是一种外在度量,而高斯曲率是一种固有度量。
尽管曲面曲率仍然是局部属性,但曲率与全局拓扑(global topology)或者“连通性”(connectedness)之间存在密切关系。Gauss-Bonnet theorem表明,高斯曲率的面积积分,或者说一个表面的总曲率正比于这个表面的亏格g。
因此,任意给定亏格g的表面,都有相同的高斯曲率积分。
有了这些定义,就可以更准确地描述表面曲率,并将其与细胞的机械生物学响应联系起来。
尽管体外生物学实验通常处理的是受限于二维平面的细胞,但细胞在体内的环境却是三维的,并且可能非常复杂。在生物体内,曲率呈现出不同的尺度,从亚细胞(曲率半径约为$10^{1}~10^{3}nm$)到超细胞尺度(曲率半径约为$10^{1}~10^{3}μm$)。本文主要关注在细胞外环境中较大尺度上出现的曲率。例如在骨组织中,破骨细胞在骨吸收过程中在矿化基质的表面上产生小凹坑,导致成骨细胞和骨细胞可以感受到局部曲率变化。然而在稍大的尺度上,骨组织还存在复杂的曲率分布,特别是松质骨。松质骨的网状结构有负的平均高斯曲率,另外由于能量最小化的骨形成过程,松质骨的平均曲率的均值接近零。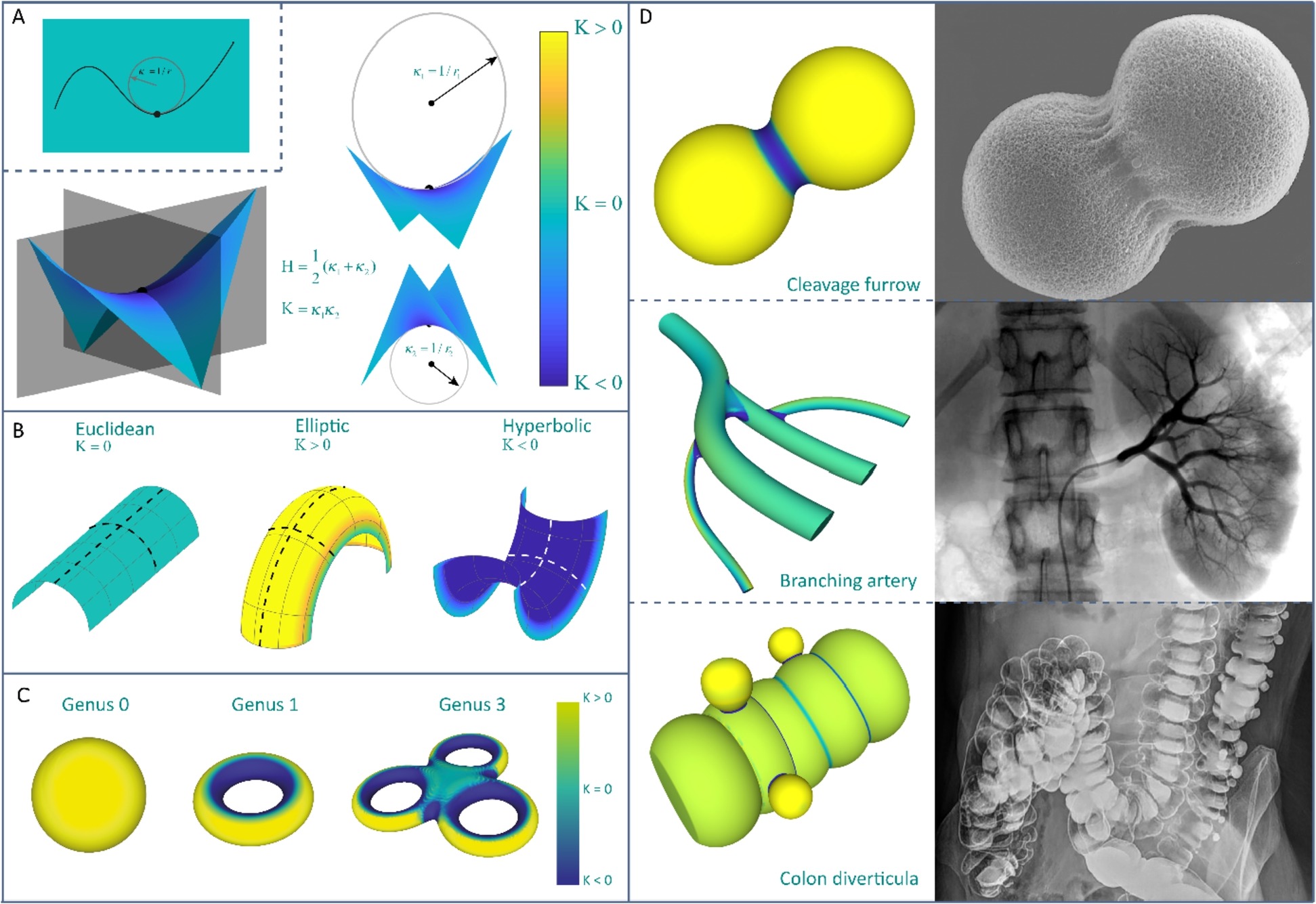
单细胞对基质曲率的响应
越来越多的实验表明,单个细胞可以以多种方式对基质曲率作出反应,包括迁移和分化。最早曲率对细胞的诱导作用被认为是contact guidance,而现在普遍认为曲率诱导是独立的一种机制。目前为止,只考虑了几种类型的弯曲形状。其中一个原因是缺少精确制造技术来控制曲率。许多研究将细胞接种在粗纤维(相当于细胞尺寸)上,或者是半圆形基质上。除了离散曲率的圆柱形,还有使用平滑变换的正弦曲线形或波浪形。这些曲面的平均曲率非零(在凸面上H>0,在凹面上H<0),但高斯曲率处处为零。另外还有半球形或者凹坑,以及交替变化的波浪形。负高斯曲率的形状很少。
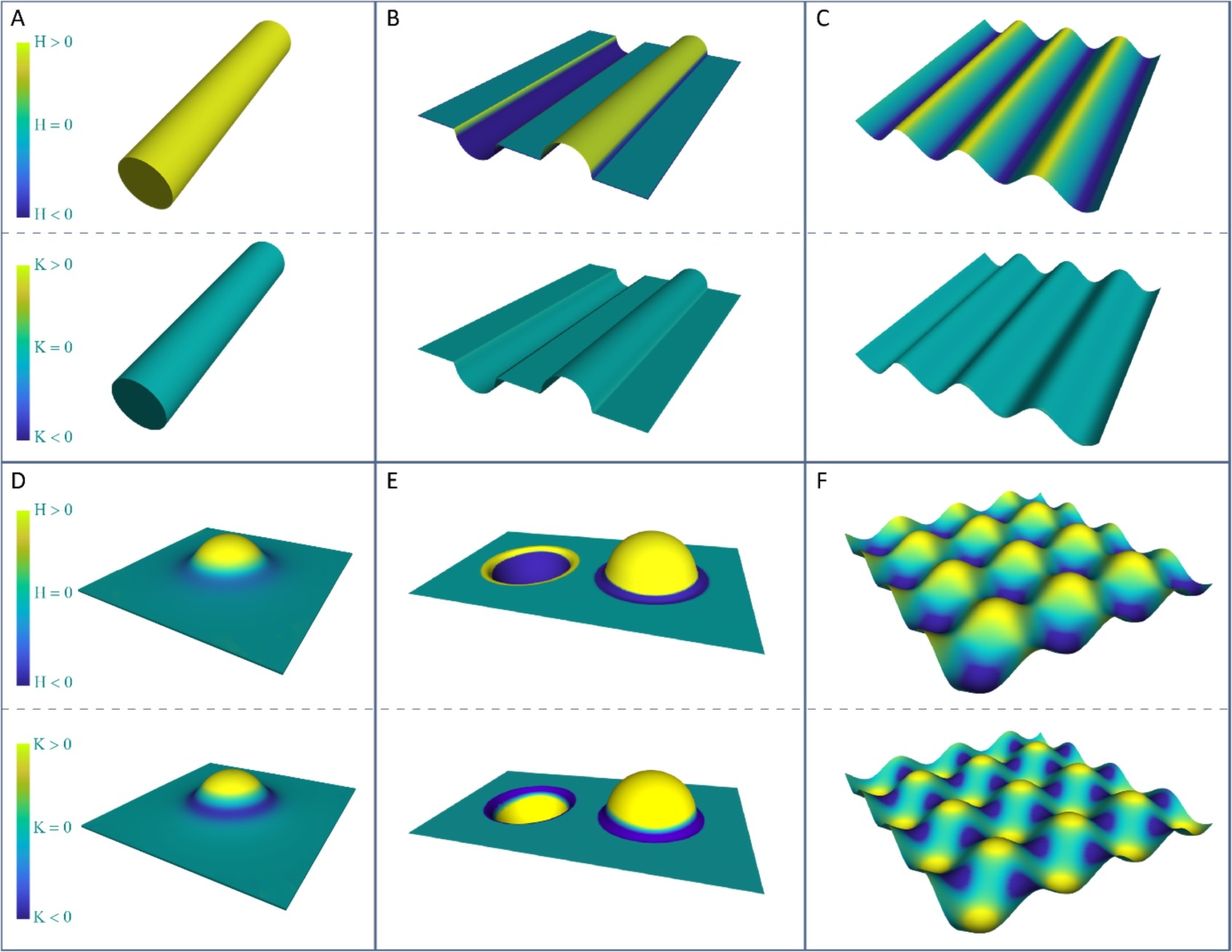
The mean (top) and Gaussian (bottom) curvature distributions of cylinders (a), hemicylindrical substrates (b), sinusoid wavy substrates (c), sphere-with-skirt substrate (d), hemispherical substrates (e), and double-sinusoid wavy substrate (f). While a-c are examples of developable (intrinsically flat) surfaces, d-f showcase non-developable (intrinsically curved) surfaces.
曲率介导细胞排列和迁移
细胞排列和迁移是在弯曲基底上进行单细胞实验中最常见的研究对象。在平坦表面上迁移的细胞,首先建立极性,在迁移方向上形成明显的前缘(front)和后缘(rear)。极化后,细胞前缘分化出片状伪足和“spiky”的丝状伪足形式的突起,通过肌动蛋白聚合来激活。随后,这些突起结合在ECM上,形成细胞骨架网络的锚定点,以施加牵引力并将细胞拉过这些锚定点。最后,细胞的后缘部分发生分离,使细胞整体移动位置。
细胞排列 alignment
成纤维细胞、平滑肌细胞和MSC在圆柱形基底上(凸起的一侧,H>0,K=0)会伸长,并且其细胞骨架沿着圆柱轴线分布。像这样,细胞倾向于沿着零曲率方向排布。在一项实验中,the degree of longitudinal alignment 随着曲率增加而增加。在球形基底上没有观察到细胞排布的倾向性,因为曲率在所有方向上都是恒定的。
细胞迁移 migration
time-lapse microscopy显示,基底曲率会影响细胞细胞的迁移方向。培养在凸的圆柱形基底(K=0,H>0)上的hBMSCs,随着基底曲率的增加,沿圆柱轴线的迁移也会增加。然而,在凹的圆柱形表面(K=0,H<0)hBMSCs没有方向性排布或者迁移。在半球形基底上,凸侧(K>0,H>0)和凹侧(K>0,H<0)呈现出不同的迁移行为。成纤维细胞和MSC在凹坑内迁移速度明显比在凸起和平坦表面更快,而在后两者上的迁移速度没有显著差异。在平滑的“双正弦”形状表面,表现出不同的平均曲率和高斯曲率,MSC和成纤维细胞始终迁移到谷(K>0,H<0)中而避开峰(K>0,H>0),且这一响应随着曲率值增加而增加。在迁移过程中,细胞核首先位于谷的最深点附近,而细胞突起则探测环境。在移动中,细胞核迅速从一个谷到另一个,并在峰上达到最大速度。凸起部分速度增加和之前的一些研究冲突,但可能这是由于平滑变化的丘陵形貌与之前的离散的半球形形貌不同导致的。细胞避开凸起(K>0,H>0)的现象很常见,条件是该曲率值足够大。例如对于成纤维细胞来说半径小于500μm的球。在巨噬细胞中也观察到了类似的现象。
尽管细胞在平坦的K=0和球形K>0表面的迁移已经有许多研究,双曲型表面K<0上的细胞行为还没有被关注。
细胞骨架力学的核心作用
在讨论细胞对弯曲基底的反应时,一个反复出现的主题是细胞骨架的排列和张力似乎起着核心作用。
细胞外环境和细胞内细胞骨架之间的机械相互作用导致了力反馈机制,该机制触发了细胞重塑其细胞骨架。当细胞位于3D弯曲的几何形状上而不是各向同性的平面基板上时,此力反馈机制将受到影响,这就是为什么在弯曲引导的讨论中细胞骨架排列和收缩力都是要考虑的重要因素。
细胞核作为曲率感受器和调节器
细胞核类似于一个粘弹性固体,比细胞骨架要硬。但是,它仍是可变形的结构。核的变形是通过以LINC(核与细胞骨架的连接子)复合体的形式通过核包膜和细胞骨架之间的紧密连接实现的。将细胞接种在平面(K=0,H=0)、凸球面(K>0,H>0)、凹球面(K<0,H<0),细胞核呈现不同的形状。在平坦和凸球形基底上,细胞核呈扁平状,在凹球形基底上细胞呈球形。对于平面上的细胞,核周肌动蛋白帽产生相对较小的压缩力,使细胞核扁平。在凸球形上,由于应力纤维的垂直排列增加,该垂直力分量增加,导致形状更加扁平。在凹球形上,因为细胞被抬离表面核压缩被释放,导致核的更接近球形。
弯曲引起的细胞核变形也与基因表达和分化有关。在高斯曲率为零的基质(即圆柱形羟基磷灰石基质)上,未观察到曲率诱导的成骨细胞分化和矿化速率的变化。然而,已经在具有非零(正)高斯曲率的基底上观察到了曲率相关的分化行为。
聚集的细胞和组织对基底曲率的响应
尽管单细胞实验提供了关于曲率感应和响应的见解,但细胞在体内通常不是独立存在的,而是在一个多细胞网络中相互联系的。细胞之间的联系可以是直接连接,如 tight junctions, gap junctions, desmosomes, and adherens junctions,或者是通过细胞-ECM粘附的间接连接。这些细胞-细胞以及细胞-ECM的相互作用建立了一种机械联系,使力能够在不同的细胞之间传递。通过这些细胞-细胞和细胞-ECM的连接,建立了一个多细胞力反馈网络,增加了细胞对环境的感知和反应范围,使它们能够合作行动。
cell sheets的曲率驱动的组织和动力学研究
细胞连接形成一个紧密结合的cell sheets/monolayer,覆盖在它们所在的基质上,使细胞能集体运作。虽然各种类型的细胞都可以形成monolayer,但大多数力学和结构的研究都集中在上皮细胞的sheet上。它们排列在体内许多三维弯曲结构的表面,如器官、囊肿和血管。除了诱导空间增殖模式外,集体组织可以使单层中的细胞感知并响应比单个细胞更弱的曲率场。有人认为这些单层细胞具有更大的 “有效长度尺度”,由于细胞-细胞连接将应力纤维连接在一起,从而形成应力纤维网络,该网络具有比单个细胞更高的弯曲能量损失。在具有更强的细胞-细胞连接和/或更高的细胞刚度的细胞片中,曲率敏感性似乎降低了,这与器官依赖性的要求有关,以最大限度地减少细胞旁运输(例如,在血脑屏障中)。在具有变化的非零高斯曲率的双正弦基底上,扩张的上皮单层在前部的前缘表现出曲率依赖性组织,其中细胞位于凹部,而不位于中央部分。有人认为,在边缘的细胞具有较高的自由度,可以根据曲率重新定位自己,而在中心部分的细胞则不具有这种自由度,因为它们之间存在相互作用上皮细胞位置的限制。
当形成monolayer时,细胞还表现出集体迁移行为,在形态发生、伤口愈合和癌症进展过程中起着至关重要的作用。圆柱外侧的上皮细胞沿纵向集体迁移,且迁移速度随曲率增加而增加。然而在空心圆柱形的内部,上皮细胞的迁移速度随曲率增加而降低,可能是由于细胞阻塞。此外,细胞可以在高曲率下从圆柱形基质上的单层前缘脱离,并切换到个体迁移模式,这种现象让人联想到上皮到间质的转变。尽管有大量证据表明弯曲的底物可指导细胞片的组织和迁移,但这并不意味着sheet可长时间保持这种几何形状。取而代之的是,细胞片可以从凹形的圆柱形基材上脱落,这种现象对于曲率增加和细胞收缩力增加来说更为深刻。细胞片脱离并不限于圆柱形的几何形状,也可以发生在非零高斯曲率的基质上。
基质弯曲不仅影响整个细胞片的组织、迁移和分离,而且还可以影响细胞片内的单个细胞。最近的证据表明,弯曲的上皮细胞中的一些细胞必须采用以前未知的数学形状,称为scutoid。
曲率驱动的富含ECM的组织形状
复杂形状的形成不只局限于sheets,还出现在三维块状的组织的构建中。细胞外基质随着三维组织生长而逐渐沉积。这种基质强化了细胞的聚集,增强了组织的负载能力。基底的几何形状,特别是曲率对组织生长的影响,主要是以osteoid-like组织作为模型系统研究的,这可能是由于临床对多孔生物材料优化的需求导致的。
继Rumpler等的开创性工作之后,一些涉及前骨细胞或间质细胞在具有特定孔隙形状的直通道内的体外研究揭示了孔隙的曲率影响组织生长的形状和动力学。更具体地说,在一个依赖于细胞-材料相互作用的初始阶段之后,孔隙曲率成为组织生长的主导因素。在具有圆形孔隙的通道中,非矿化组织均匀地向内生长,曲率较高的地方组织更厚,静态和灌注条件下的矿化组织也得到了类似的结果。在非圆形通道中(如三角形或方形截面),组织生长首先发生于角落(即高曲率区域),而最初在平坦的侧面没有组织形成。随着组织逐渐沉积在角部,孔隙变圆,平坦面的局部几何形状被改变,组织也开始在这些位置生长。随着时间的推移,这将形成一个圆形的组织前沿,均匀地向内生长。在具有凸多边形孔的通道中,角部的组织生长速度随着角部曲率的增加而增加,也就是说三角形孔的角部比方形或六边形孔的角部要高。尽管如此,具有相同周长的凸孔的平均生长速度与它们的形状无关,这是因为在凸多边形中,平均曲率和平均生长速度与周长成反比。然而,在具有凹形多边形截面的通道中,如十字形,由于十字形(8个凹角)与正方形(4个凹角)相比有更多的 “生长诱导 “角,因此初始总生长速率可以明显高于正方形(凸形)形状。这意味着人工组织支架的孔隙几何形状不仅要优化质量传输和力学性能,而且要优化所需的组织生长速度。

这些直孔通道,无论其截面形状是凸的还是非凸的,都属于 “广义圆柱体”(K=0),其平行的ruling lines在一个方向上是弯曲的,但在另一个方向上保持平坦。其他的例子是半圆柱体、开放的通道或波浪形的基体,它们只在一个方向上弯曲。关于这种几何形状的一个普遍和重要的观察是,组织主要形成在凹区域(H<0),初始时几乎没有组织沉积在凸区域(H>0)。例如,在半圆柱形通道中,组织逐渐在凹部生长,有效地使圆柱形腔体 “扁平化”。此外,组织的生长速度明显低于相同半径的全圆柱形通道,这是由于凸形边界的存在,在局部几何形状因组织前沿的推进而变成凹形之前,其上不会形成组织[131]。在波浪形基底上,表现出凸和凹区域的交替模式(即正和负的平均曲率),组织也几乎只在凹区域内生成。
为什么组织采用这些特殊形状?可以阐明这一问题的一致观察结果是,组织的形状让人联想到粘性流体将采用的形状。生物材料的出现形状与物理学驱动的无生命材料中的观察结果有些相似,如润湿液滴、肥皂泡或其他涉及液体界面的系统。例如,发育中的果蝇视网膜中锥体细胞的图案形成与肥皂泡聚类表现出惊人的相似性。驱动这些无生命材料形状形成的基本物理机制是表面或界面张力的最小化,导致表面积趋于最小化。由于液体和生物形状形成之间的明显相似性,在足够长的时间尺度上,组织被称为像具有一定表面张力的粘性液体一样。因此,组织在弯曲基质上的出现组织通常被归结为表面张力最小化,尽管其他因素也在发挥作用。形状和表面张力之间的关系由Young-Laplace方程决定,该方程指出,在流体界面上持续的压力差(Δp)与表面张力(σ)和平均曲率(H)成正比。
Δp=2σH
事实上,Young-Laplace方程或其稍加修改的版本已被用于描述平坦基底上离散部位的细胞和组织的形状,也包括生长在弯曲基底上的骨样组织的形状。虽然液体中的张力是由各种分子间的内聚力相互作用(如范德华力)导致的,但组织张力的起源已经用不同的理论来解释,如 “差异粘附假说”,但似乎同时涉及细胞间粘附和皮质收缩力。在体外曲率驱动的结缔组织生长中,界面张力的指标是以强壮的肌动蛋白纤维的形式提供的,这些纤维与组织-介质界面高度一致。此外,尽管整个组织体积的细胞密度均匀,但靠近组织-中间界面的肌动蛋白密度较高。据推测,肌动蛋白在组织前端的集体排列可能导致净法向力指向远离表面,从而推动组织前端的进一步推进。此外,存在于生长前沿的高张力可以诱导细胞转换,如成纤维细胞和肌成纤维细胞之间的可逆转换,这对伤口愈合至关重要。除了细胞尺度的肌动蛋白取向外,合成的细胞外基质中的胶原纤维也遵循同样的排列方式,这也表明了组织层面的组织。事实上,随着组织的发展,细胞骨架收缩产生的拉力逐渐转移到胶原纤维上,从而形成一个永久受力的基质,可以部分接管细胞产生的部分拉力。在马鞍形基质(K<0)上,肌动蛋白纤维已被证明表现出奇异性,并大致沿局部零曲率方向排列。这可能潜在地表明了一种能量上有利的取向顺序,符合最近的假说,即组织可以表现得像active nematic liquid crystals,而细胞是nematic agents,尽管需要更多的证据来证实这一假说。
大多数曲率驱动的组织生长研究都是在体外进行的,然而一些体内结果也表明,曲率在组织形成的组织和动力学中起着一定的作用。在体内用于治疗大面积骨缺损的支柱型支架中,发现纤维组织的形成受支架几何形状的引导,纤维在圆柱形支柱之间排列和跨越。此外,发现新形成的血管在植入后的初始阶段主要位于骨植入物的凹陷区域(H<0),可能表明骨再生过程中曲率引导的血管生成。最近,利用带有水平支柱的0/90°支架,表明支架曲率驱动体内软组织形成,并观察到一个新的基质矿化过程。更具体地说,组织生长是在平均曲率较高的支架区域开始的,并且可以使用曲率驱动的组织生长模型进行有效预测。
总之,力学和几何学之间的相互作用超越了单个细胞的水平,在塑造更复杂的多细胞组织构造中也起着重要作用。在单层细胞片的情况下,如上皮单层,基底曲率,细胞-细胞粘附和集体片收缩之间的平衡可能会影响集体迁移,片脱落,甚至单个细胞的形状。此外,这些薄薄的细胞片可能会弯曲、起皱或从平坦的状态折叠成复杂的、弯曲的形状,以响应外部施加的载荷(可能由内部预应力平衡)。在富含ECM的组织(如骨样组织)的情况下,当组织在3D(弯曲)环境中生长时,可以观察到明显的液体样行为。一般来说,这类组织优先生长在凹面区域(例如,在直面孔的角落区域),导致细胞外的几何形状逐渐平滑,被新细胞感知。这些生长的组织表现出具有排列的肌动蛋白纤维的细胞(主要在组织前端)。在沉积的ECM纤维中也观察到类似的排列。因此,在这些富含 ECM 的组织中观察到的液态形状与表面张力的概念有关。因此,机械原理似乎以类似于弯曲基质上单细胞的时空组织的方式来控制组织层面的大部分形状形成。虽然通过细胞-细胞或细胞-ECM相互作用的力传递和长程细胞骨架重塑无疑在这种新出现的组织中发挥了关键作用,但还需要更多的见解来揭示细胞级组织如何转化为组织级组织。