扩散方程简介
一维扩散方程可以表示为
其中,$ \Phi $为因变量(如温度、质量和动量等),表示在无限长介质中沿着x轴正负两个方向相同概率的扩散。扩散速率取决于参数$ \alpha $,对于能量扩散、质量扩散和动量扩散,$ \alpha $分别代表热扩散系数、质扩散系数和运动学黏度等。上述方程在空间上具有二阶导数,扩散发生在两个方向上,需要两个边界条件。同时该方程在时间上是一阶导数,因此在时间上扩散是单方向的。
格子玻尔兹曼方法
分布函数的动力学方程$ f_{k}(x, t) $可写成
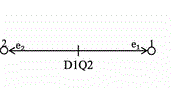
其中,k=1,2(对于一维问题D1Q2)。方程左边表示迁移过程,分布函数沿着格子的迁移速度为$ c_{k}=\frac{\Delta x}{\Delta t} $;方程右边项$ \Omega _{k} $表示碰撞过程分布函数$ f_{k} $的变化速率。
对碰撞算子采用BGK近似可得
$ \tau $表示到达平衡分布$ f_{k}^{eq}(x,t) $所需要的松弛时间,与宏观尺度的扩散系数有关。采用BGK近似,上述动力学方程可以离散为
将$ \Delta x = c_{k}\Delta t $带入上式中可简化为
上述方程就是一维空间内扩散问题的计算式,也可以表示为
其中,$ \omega =\frac{\Delta t}{\tau } $为松弛频率。
在实际计算中通常表示为两个步骤:迁移和碰撞
(1)碰撞
(2)迁移
扩散方程中的因变量$ \Phi $与分布函数$ f_{i} $相关,即
平衡分布函数$ f_{k}^{eq}$ 可选择为
其中$ w_{k} $表示k方向的权重因子,权重因子需满足$ \sum_{k=1}^{2}w_{k}=1 $。
分布函数沿各个方向求和可得
$ \alpha $与$ \omega $的关系可以通过Chapman-Enskog展开得到
D为问题的维数(D=1表示一维,D=2表示二维,D=3表示三维)。
边界条件
在左侧边界x=0,$ f_{2}$可由迁移过程获得,则左侧仅有一个未知量$ f_{1}$。因此需要一个方程用于描述$ f_{1} $与已知参数的关系,从而求解出$ f_{1} $。右侧边界x=L,$ f_{1} $可以由迁移过程获得,需要确定$ f_{2} $。下面讨论不同边界条件的处理。
恒温边界条件
对D1Q2模型,在边界x=0处通量平衡的描述为
其中$ f_{1}^{eq}(0,t)=w_{1}T_{w}=0.5T_{w} $,$ f_{2}^{eq}(0,t)=w_{2}T_{w}=0.5T_{w} $。因此在x=0处,$ f_{1}(0)+f_{2}(0)=T_{w} $,$ f_{1}(0)=T_{w}-f_{2}(0) $。
绝热(无热流密度)边界条件
温度梯度为0,意味着
因此
或
m表示最后的格子节点。
举例
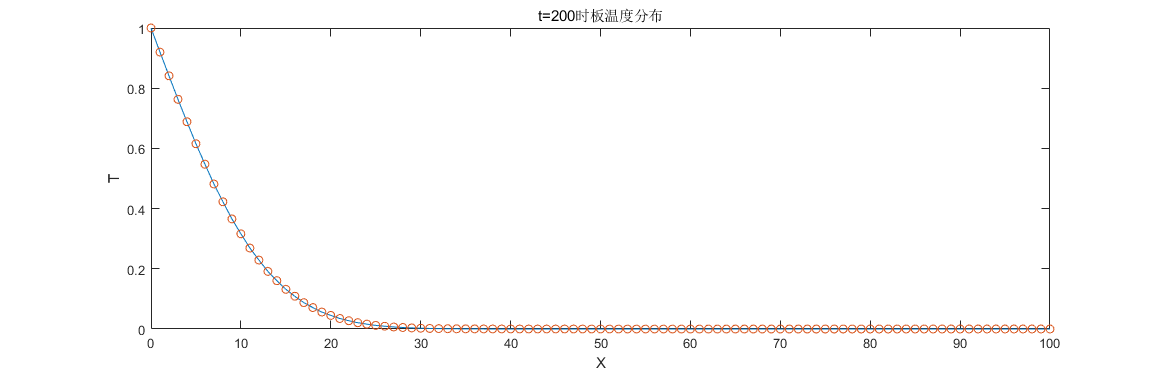
下面用一个具体的例子来说明。对于无限大板中的热扩散问题,假设板的初始温度$ T=0 $,当时间$ t\geq 0 $时,板左侧面受到高温$ T=1.0 $,板长为100。设$ \alpha =0.25$,计算t=200时板中的温度分布。
解:首先离散化时间和空间,$ \Delta x = 1.0$,$ \Delta t = 1.0$。根据前述方程,$ 0.25 = \frac{1}{\omega}-0.5 $,得$ \omega =1.333333$。权重因子$ w_{k}=0.5, k=1,2 $。
matlab代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59% 一维扩散问题 D1Q2
m = 100;
f0 = zeros(1,m+1);
f1 = f0;
f2 = f0;
rho = f0;
feq = f0;
x = f0;
dt = 1;
dx = 1;
x(1) = 0;
for i = 2:m+1
x(i) = x(i-1) +dx;
end
csq = dx*dx / (dt*dt);
alpha = 0.25; % 扩散系数
omega = 1.0 / (alpha / (dt*csq) + 0.5); % 松弛频率
mstep = 200; % 迭代次数
twall = 1.0; % 左边界温度
% 初始化
for i = 1:m+1
rho(i) = 0.0;
f1(i) = 0.5*rho(i);
f2(i) = 0.5*rho(i);
end
% 主循环
for k = 1:mstep
% collision
for i = 1:m+1
rho(i) = f1(i) + f2(i);
feq(i) = 0.5*rho(i);
f1(i) = (1-omega) * f1(i) + omega*feq(i);
f2(i) = (1-omega) * f2(i) + omega*feq(i);
end
% streaming
for i = 2:m
f1(m+2-i) = f1(m+1-i);
f2(i-1) = f2(i);
end
% boundary condition
f1(1) = twall - f2(1);
f1(m+1) = f1(m);
f2(m+1) = f2(m);
end
% 绘制温度分布图
plot (x, rho)
hold on
plot(x, rho,'o')
title ('t=200时板温度分布')
xlabel('X')
ylabel('T')
计算结果如下图: