matlab绘制水滴形曲线并计算曲率

问题描述

在matlab中，利用贝塞尔曲线绘制闭合的水滴形曲线，并计算曲线上各点的曲率。

基础知识

贝塞尔曲线

在之前的博客中已经介绍过贝塞尔曲线的基本形式（详见贝塞尔曲线简介）。由于水滴形曲线是一条闭合曲线，需要首尾两个控制点重合，另外中间至少还需要两个位置不同的控制点，则一共需要四个控制点，因此选择三阶贝塞尔曲线来实现。

曲率定义

对于一条光滑曲线C，曲线C上从点M到M’的弧为Δs，切线的转角为Δα。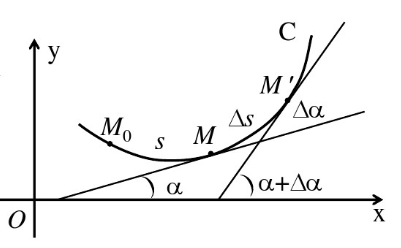
曲率定义

平均曲率：定义 $\bar{K} = \left | \frac{\Delta\alpha}{\Delta s} {} \right |$ 为弧段 ${M{M}'}$ 的平均曲率。它反映了弧 ${M{M}'}$ 的平均弯曲程度。

曲率：称 $K=\lim_{\Delta s\rightarrow 0}\left | \frac{\Delta \alpha }{\Delta s} \right |$ 为曲线C在点M处的曲率。

在 $\lim_{\Delta s\rightarrow 0} \frac{\Delta \alpha }{\Delta s} = \frac{d\alpha }{ds}$ 存在的条件下， $K = \left | \frac{d\alpha }{ds} \right |$ 。此式即为曲率的计算公式。

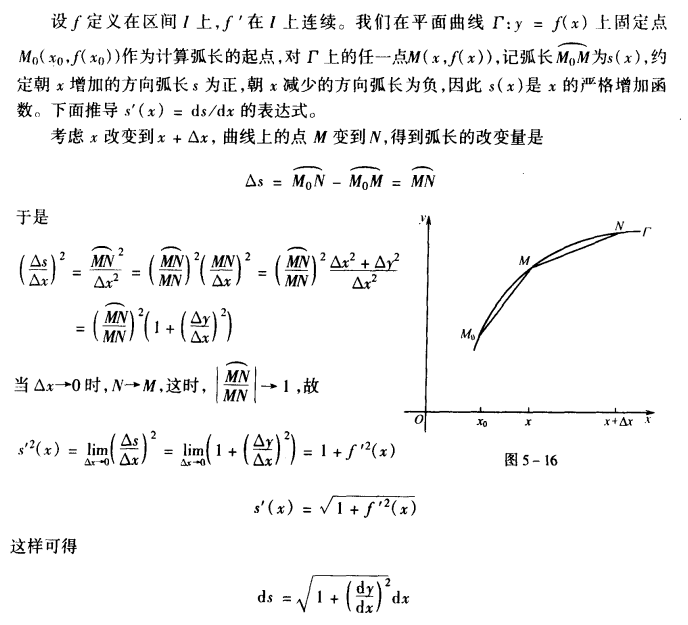
设曲线的直角坐标方程是 $y=f(x)$ ，且 $f(x)$ 具有二阶导数。因为 $tan \alpha = {y}'$ ，所以 $sec^{2}\alpha \frac{d\alpha }{dx} = {y}''$ ，又知 $ds=\sqrt{1+{y}'^{2}}dx$ （弧微分公式），从而有

$K = \frac{\left |{y}'' \right |}{(1+{y}'^{2})^{3/2}}$

补充：
弧微分公式推导

刘景麟，黄振友编《微积分上》国防工业出版社 2006

对于参数方程，可以采用同样的推导方法求出曲率计算公式。若参数方程形式为 $\left\{\begin{matrix} x=\phi (t)\\ y=\omega (t) \end{matrix}\right.$ ，则曲率的计算公式为 $K = \frac{\left | {\phi}' (t){\omega}'' (t)-{\omega}' (t){\phi}'' (t) \right |}{\left [ {\phi}'^{2} (t) + {\omega}'^{2} (t) \right ]^{3/2}}$ 。

matlab绘制曲线

首先定义四个控制点的坐标，然后根据三阶贝塞尔曲线方程计算对应于参数t的x, y值。这里设置步长为0.01。

% 控制点坐标
P0 = [0;0];
P1 = [-1;1.4];
P2 = [1;1.4];
P3 = [0;0];

% 计算x, y
t = 0:0.01:1;
x = P0(1)*(1-t).^3 + 3*P1(1).*t.*(1-t).^2 + 3*P2(1).*t.^2.*(1-t) + P3(1).*t.^3;
y = P0(2)*(1-t).^3 + 3*P1(2).*t.*(1-t).^2 + 3*P2(2).*t.^2.*(1-t) + P3(2).*t.^3;

% 绘图
figure(1)
plot(x, y)
axis equal

绘制的结果为
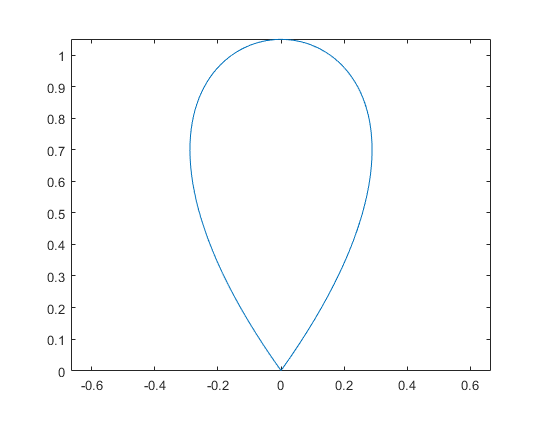
水滴形曲线

matlab计算曲率

根据曲率计算公式，首先需要计算x, y对t的一阶和二阶导数，可以用定义符号变量的方法计算。

首先定义t为符号变量，计算x, y的符号表达式。

1
2
3

syms t;
phi = P0(1)*(1-t).^3 + 3*P1(1).*t.*(1-t).^2 + 3*P2(1).*t.^2.*(1-t) + P3(1).*t.^3;
omega = P0(2)*(1-t).^3 + 3*P1(2).*t.*(1-t).^2 + 3*P2(2).*t.^2.*(1-t) + P3(2).*t.^3;

此时可以看到t, phi, omega都是sym类型的变量。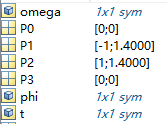
符号变量

然后求phi和omega的一阶、二阶导数。

phi1 = diff(phi);
omega1 = diff(omega);
phi2 = diff(phi1);
omega2 = diff(omega1);

最后根据公式计算曲率K，并将符号表达式转换为数值。其中subs是符号替换函数，可以将符号表达式中的某些符号变量替换为指定的新变量。调用方式为：subs(s, old, new)，将所有的old换成new，并计算s，返回s。需要注意的是subs返回的仍然是符号表达式，需要用double函数再转化为数值类型。

1 2	k = (abs(phi1.omega2 - omega1.phi2) / (phi1.^2 + omega1.^2).^(1.5)); k1 = double(subs(k,t, 0:0.01:1));

k1中保存的变量就是对应于t=0到1共101个点的曲率值。

其他

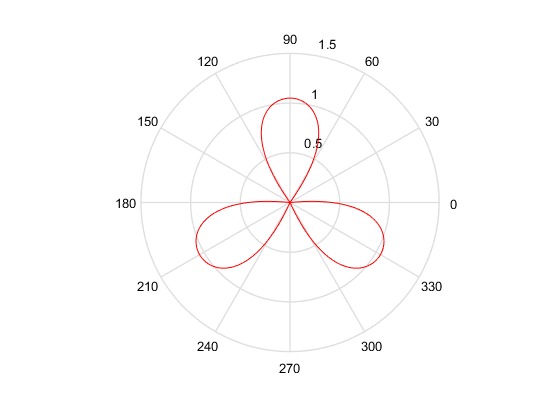
如果想要画一个以水滴形顶点为圆心，分别旋转120°、240°，形成三个水滴组成的旋转对称图案，可以将x, y转化成极坐标，并绘制极坐标图。cart2pol函数可以将笛卡尔坐标转换为极坐标。

[TH,R] = cart2pol(x, y);
polar(TH,R,'r');
hold on
TH2 = TH+120/180*pi;
polar(TH2,R,'r');
hold on
TH2 = TH+240/180*pi;
polar(TH2,R,'r');

最终结果如图：
三个水滴