贝塞尔曲线简介

贝塞尔曲线（Bézier curve）属于经常听说但又不知道到底是什么的一类词。偶然需要用到，就简单地了解并在这里记录一下。

贝塞尔曲线的应用非常广泛，如矢量图和位图，实际上贝塞尔曲线常常用在矢量图软件中，用于绘制曲线。另外PhotoShop里唯一的矢量绘制工具——钢笔工具，就采用了贝塞尔曲线。

历史

贝塞尔曲线的数学基础是伯恩斯坦多项式，1912年以来就为人所知。后来在19世纪60年代法国工程师Pierre Bézier将它应用在雷诺汽车的车身曲线设计上，并广泛宣传这些多项式，贝塞尔曲线从此得名并被广泛应用。

定义和实例

贝塞尔曲线由一组控制点定义，并且生成的曲线完全包含在其控制点的凸包中，因此可以以图形方式显示这些点并用于直观地操纵曲线。

设控制点为P₀到P_n，n称为它的阶数。第一个和最后一个控制点始终是曲线的端点，但是中间控制点（如果有的话）通常不在曲线上。

这里有一个动态绘制贝塞尔曲线的在线演示，可以自己设置控制点的个数和位置，观察曲线的轨迹。
（在线演示链接来源：前端乱炖 贝塞尔曲线扫盲 http://www.html-js.com/article/1628)

线性贝塞尔曲线 Linear Bézier curves

给定两个不同的点P₀和P₁，线性贝塞尔曲线是这两点之间的直线。曲线由下式给出：

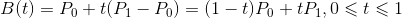
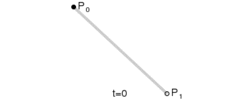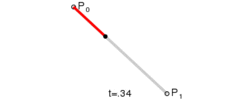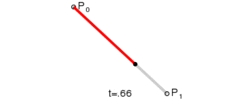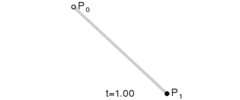
实际上相当于线性插值。

二阶贝塞尔曲线 Quadratic Bézier curves

二阶贝塞尔曲线是函数B(t)经过的路径，由控制点P₀，P₁和P₂给出。

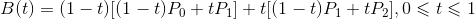
可以理解为从P₀到P₁和从P₁到P₂的线性贝塞尔曲线上对应点的线性插值。上式整理可得：

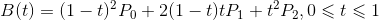
二阶贝塞尔曲线对t的导数是

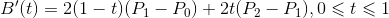
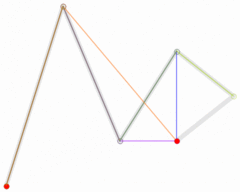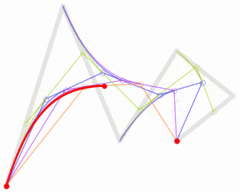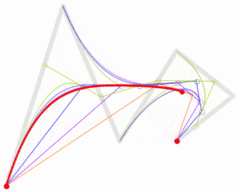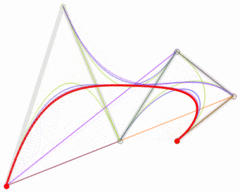
从中可以得出结论，曲线在P₀和P₂点的切线相交于P₁。

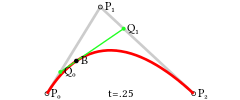
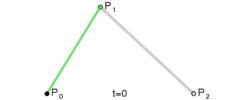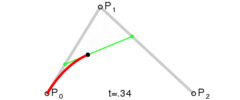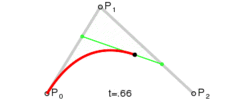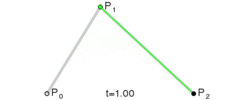
图中，P₀Q₀/P₀P₁ = P₁Q₁/P₁P₂ = Q₀B/Q₀Q₁。

三阶贝塞尔曲线 Cubic Bézier curves

以此类推，三阶贝塞尔曲线由四个点P₀，P₁，P₂和P₃定义。曲线的形式是：

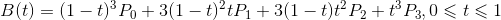
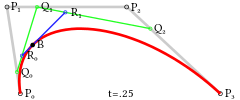
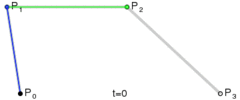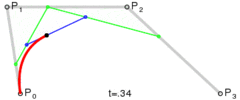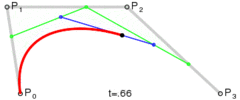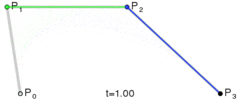
当需要更复杂的曲线时，只需要增加控制点的个数。比如下图红色曲线显示的是五阶贝塞尔曲线。